Ecuación general o implícita
Deduciremos la ecuación general de la recta a partir de la ecuación continua
=u_1(y\;-\;p2)\;\Rightarrow)



Ecuación general o implicita de la recta

Teniendo en cuenta el cambio de variable que se ha hecho para llegar a la fórmula de la ecuación general se cumple que un vector de dirección de la recta es
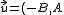)
Asímismo un vector normal a la recta es
)
Halla la ecuación general de la recta que pasa por P(-1,-4) y cuyo vector de dirección es
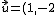)
.
Como un vector de dirección es
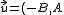)
entonces

.
La ecuación general será de la forma

.
Ahora imponemos que P pertenece a la recta sustituyendo sus componente en la ecuación
-(-4)+C=0\;\Rightarrow\;2+4+C=0\;\Rightarrow\;C=-6)
Luego la ecuación pedida es

Consideremos la recta

. Halla la ecuación de la recta perpendicular a r que pasa por el punto P(1,1).
Como la recta que buscamos es perpendicular a r, un vector normal a r
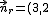)
es un vector de dirección de la recta buscada. Por tanto

siendo la ecuación de la forma

, ahora imponemos que pasa por P, sustituyendo sus componentes en la ecuación

La ecuación general de la recta perpendicular a r que pasa por P es
