Teorema del coseno
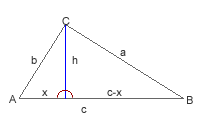
Dado un triángulo cualquiera, trazamos una altura h que dividirá el triángulo en dos triángulos rectángulos.
Si aplicamos el teorema de Pitágoras a cada triángulo rectángulo se tiene
b 2 = h 2 + x 2, por tanto
h 2 = b 2 - x 2
a
2 = h 2 + (c - x) 2, por tanto
h 2 = a 2 -(c - x) 2
Igualando el valor de
h 2
b 2 - x 2 = a 2 -(c - x) 2
Si en la ecuación anterior despejamos
a 2 queda
a 2 = b 2 + c 2 - 2cx
Por otro lado, tomando el triángulo rectángulo de la izquierda se cumple que
x =b·CosA
Sustituyendo se llega a la igualdad que se conoce como Teorema del Coseno.
Esta igualdad es independiente del lado que se tome.
Gracias al teorema del coseno se puede resolver un triángulo cualquiera conocidos dos lados y el ángulo que lo forman.
También se puede resolver un triángulo del que se conozcan los tres lados, sin más que despejar el coseno del ángulo
que se quiera