Variaciones con repetición

Sea A un conjunto con m elementos. Llamamos variaciones con repetición de n elementos tomados de m en m a todas a las agrupaciones que podemos hacer con m elementos de A independientemente de que se repita alguno.
El número de variaciones con repetición viene dado por:

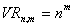Características:

• Se consideran grupos distintos aquellos con los mismos elementos en distinto orden.
• Cualquier elemento se puede repetir.

Observación: En el caso de variaciones sin repetición los grupos que podíamos formar eran inferiores al total de elementos. Ahora podemos tomar conjuntos con más elementos ya que podemos repetir.

Ejemplos:

• ¿Cuántos números de 8 cifras que empiecen por 6 se pueden formar?
Si los números empiezan por 6 sólo queda determinar qué ocurre con las siete últimas cifras que puede cualquier dígito.

Se Podrán formar 10.000.000 números.


• ¿Cuántas apuestas distintas se pueden hacer en la quiniela para cubrir todas las posibilidades? Nota: Incluido el pleno al 15.
Para rellenar una quiniela usamos tres signos 1,X,2, luego tenemos tres elementos. Se rellenan 15 casillas, por tanto los agrupamos de 15 en 15.
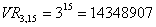apuestas.