Resolución de triángulos rectángulos

Resolver un triángulo consiste en averiguar las medidas de sus tres ángulos y tres lados. Con el añadido de que uno de los ángulos ya se conoce, es 90º. La información mínima que necesitamos para resolver el triángulo es que conozcamos dos lados del triángulo o que conozcamos un ángulo (distinto del recto) y un lado. Veámos como se resuelve el triángulo en cada caso.

Conocidos dos lados del triángulo
Si conocemos dos lados del triángulo rectángulo, se determina el tercero usando el teorema de Pitágoras, una vez hallado el lado que falta se determina el seno, coseno o tangente de un ángulo cualquiera y a través de la función inversa se halla el ángulo, el último ángulo se halla teniendo en cuenta que las uma de los ángulos de un triángulo es 180º.

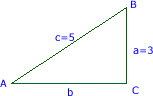
Vamos a resolver el triángulo de la figura.
En virtud del teorema de Pitágoras se sabe que
c² = a² + b², por tanto b ² = c ² - a ² ;
b ² = 5 ² - 3 ² ; b ² = 25 - 9 ; b ² = 16 ; b = 4.
Ahora que ya tenemos los tres lados calculamos los ángulos ayudandonos de las razones trigonométricas:
senA=3/5 por tanto A=arcsen(3/5) ; A= 36'87º, como A+B+C=180º y C=90º, entonces B=180º -90º-36'87º ; B= 53'13º
En resumen: Los lados del triángulo son 3,4,5 y los ángulos 90º, 36'87º y 53'13º.

Resuelve el siguiente triángulo

						=
		=10
						=
	=			=5		=

Nota: Los ángulos se expresan en grados y sólo en grados (25º30' = 25.5º). Redondea los resultados a dos cifras decimales. No tiene porqué haber relación directa entre el valor de los datos y la figura, esta última es meramente orientativa.