Introducción

Si consideramos el plano Euclideo, éste está formado por un conjunto de puntos. Si queremos identificar unívocamente cada uno de estos puntos hemos de fijar un sistema de referencia formado por un punto O (origen) y una base de V
2 (espacio vectorial de dimensión 2). De todas las posibles bases vamos a tomar una ortonormal B=(i,j).
Fijado el sistema de referencia R={O,i,j} cualquier punto del plano queda identificado. Usualmente O=(0.0) i=(1,0) j=(0,1).
En el plano cada punto P tiene las mismas coordenadas que el vector

en la base B.
+(1,0)+2(0,1)=(1,2))
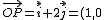+2(0,1)=(1,2))
En el plano Euclídeo podemos encontrar dos subvaridades lineales, puntos y rectas. Es conveniente conocer la expresión analítica de una recta, esta expresión se puede determinar a partir de dos puntos, un punto y un vector de dirección o un punto y la pendiente.