Números combinatorios

Llamaremos número combinatorio a donde .
Los números combinatorios tienen una serie de propiedades que son dignas de reseñar:

• Los números combinatorias son simétricos, es decir,


• 
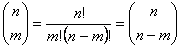
  Prueba



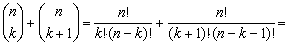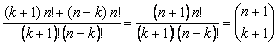
• Aplicación de los números combinatorios al desarrollo de la n-ésima potencia de un binomio. Binomio de Newton.
  
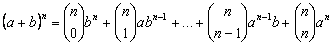
  o de forma contraida
  
  
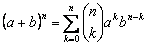
Esta igualdad nos permite desarrollar cualquier potencia de un binomio.



.
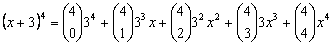
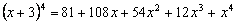
Basta con notar que 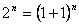y aplicar el binomio de Newton
• Triángulo de Tartaglia.
Vamos a construir un triángulo con naturales, empezando por el 1, valor que también tendrán los extremos de cada línea que formemos. Por otro lado, cada valor interior será el resultado de sumar los valores inmediatos superiores. Es construcción tienen por primeras filas las que siguen:

									1
								1		1
							1		2		1
						1		3		3		1
					1		4		6		4		1
				1		5		10		10		5		1
			1		6		15		20		15		6		1

A esta formación se le llama triángulo de Tartaglia, en honor a NicolaFontana, que era un poco tartaja, de ahí lo de Tartaglia.
Esta disposición de números coincide con los números combinatorios Una aplicación sencilla del triángulo de Tartaglia es la determinación de la potencia n-ésima de un binomio.

Como podemos observar los coeficientes del desarrollo del binomio coinciden con los valores de la fila del triángulo de Tartaglia para la que se toman combinaciones de 5 elementos.