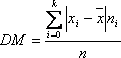Medidas descriptivas
Desviación media
Las medidas de dispersión como el
rango o el rango intercuartílico son poco significativas y sólo se apoyan en dos datos, sería conveniente tener una medida de la dispersión de los datos respecto a la media (valor en el que se resumen todos los datos) y en la que tomásemos información de todas la observaciones.
Una medida para conocer la dispersión de los datos sería ver que errores se comenten al dar la media en lugar del auténtico valor, en el valor i-ésimo cometeríamos un error
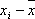
.
Si sumamos todas las desviaciones
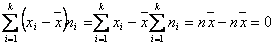
. Se compensan las desviaciones positivas y negativas, por lo no podemos conocer la desviación. Para corregir ese problema podemos considerar todos los errores que calculemos como positivos, para ello basta con tomar el valor absoluto, si además consideramos la media de esos errores obtenemos la desviación media.
Definimos la desviación media como
donde
n1 + n2 +...+ nk = n.
Propiedades
- Nos da la media de la dispersión de los datos.
- Intervienen para su cálculo todos los datos.
- Cada vez que insertemos un dato nuevo se modificará.
- Al intervenir un valor absoluto los cálculos son complicados.
- A mayor concentración de los datos entorno a la media menor será su valor.
- DM es no negativa
- DM=0 si y sólo si todos los valores son coincidentes.