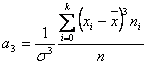|
|
Medidas descriptivas
Documento sin título
Coeficiente de asimetría
Además de conocer las medidas de tendencia central y dispersión sería conveniente conocer cómo están distribuidos dos datos en torno a las medidas de tendencia central.
Una distribución de frecuencias puede ser simétrica o asimétrica. Para saber si es simétrica tenemos que tomar una referencia, es decir, ver respecto a qué es simétrica, nosotros vamos a estudiar la simetría respecto a la media, para ello usaremos el siguiente coeficiente de simetría:
- Si a3 = 0 diremos que la distribución es simétrica, en ese caso las desviaciones a la derecha y a la izquierda de la media se compensan.
- Si a3 < 0 entonces
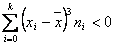 las frecuencias mayores están a la izquierda de la media por lo que queda la cola a la derecha, diremos que la distribución está sesgada a la izquierda o que es asimétrica negativa. las frecuencias mayores están a la izquierda de la media por lo que queda la cola a la derecha, diremos que la distribución está sesgada a la izquierda o que es asimétrica negativa.
- Si a3 > 0 entonces
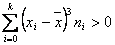 las frecuencias mayores están a la derecha de la media por lo que queda la cola a la izquierda, diremos que la distribución está sesgada a la derecha o que es asimétrica positiva. las frecuencias mayores están a la derecha de la media por lo que queda la cola a la izquierda, diremos que la distribución está sesgada a la derecha o que es asimétrica positiva.
Propiedades
- No depende de las unidades de medida de las variables.
- Es invariante ante el cambio de escalas
|
|