Teorema del seno
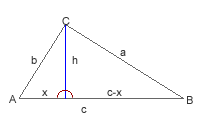
Dado un triángulo cualquiera, trazamos una altura h que dividirá el triángulo en dos triángulos rectángulos, en ca da uno de ellos se tiene que:
h=b·senA
h=a·senB
Igualando
b·senA = a·senB
Razonando igual con los ángulos B y C, se tiene que
b·senC=c·senB

En el caso de que el triángulo sea obtusángulo, queda una altura fuera del triángulo y se llega a la misma conclusión.
h=b.senC
h=c·sen(180º-B) => h=c·senB
(al ser B y 180º-B suplementarios)
En virtud de los expuesto anteriormente y reordenando las igualdades se tiene que la razón entre cada lado y el seno del ángulo opuesto es constante, a esta igualdad se la conoce como el teorema del seno