Teorema del resto
Evaluar un polinomio
Evaluar un polinomio consiste en determinar qué valor toma el polinomio cuando la indeterminada
(x) se sustituye por un número.
Consideramos el polinomio P(x)=2x3-5x+3 evaluar el polinomio en 1 consiste en sustituir la indeterminada por 1 (x=1) quedando P(1)=2·13-5·1+3=2-5+3=0.
Teorema del resto
El valor que se obtiene al evaluar un polinomio en
x=a coincide con el resto de dividir ese polinomio por
x-a.
Si dividimos un polinomio
P(x) por
x-a se obtendrá un cociente
C(x) y un resto
r.
En toda división el dividendo
P(x) es igual al divisor
x-a por el cociente
C(x) más el resto
r , es decir,
P(x)=(x-a)·C(x) + r.
Al evaluar el polinomio en el punto se tiene
P(a)=(a-a)·C(a) + r , como
a-a =0 entonces
P(a) = r
Gracias a este teorema podemos usar la regla de Ruffini para evaluar un polinomio en un punto.
Evalúa el polinomio
P(x)=2x3-5x+3 en
x=1 usando la regla de Ruffini
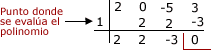P(1) = 0 ya que 0 es el resto de la división de
P(x) entre
x-a 
