Vector normal del plano
Un plano se puede caracteriazar por un punto y dos vectores de dirección o bien por un punto y su vector normal (perpendicular al plano)
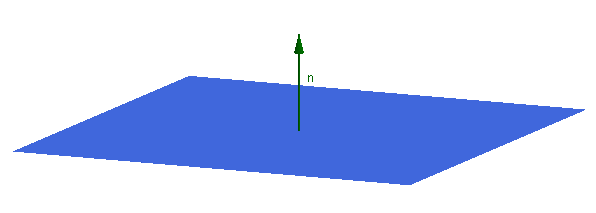
Supongamos que tenemos un plano

y dos puntos en él
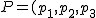\;Q=(q_1,q_2,q_3)\;)
.
Como


+B(p_2-q_2)+C(p_3-q_3)=0)
Por otro lado se tiene que
)
Se sabe que dos vectores son ortogonales si y solo si su producto escalar es nulo
+B(p_2-q_2)+C(p_3-q_3)=0\;\Rightarrow\;(A,B,C)\perp\vec{QP})
Luego el vector (A,B,C) es perpendicular a cualquier vector director del plano, esto significa que si tenemos la ecuación general del plano, los coeficientes de las incógnitas forman un vector normal al plano
)
Halla la ecuación implícita del plano que pasa por el punto P(0,-1,2) y que es perpendicular a la recta

Como la recta es perpendicular al plano, el vector director de la recta es un vector normal del plano, es decir,
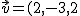)
serán los coeficientes de las variables,
=(2,-3,2))
.
Ahora queda por determinar el término independiente D, que podemos calcular imponiendo que P tiene que cumplir la ecuación del plano
Así la ecuación implícita del plano es
