Asíntota vertical.
Una recta es una asíntota vertical de una función si o

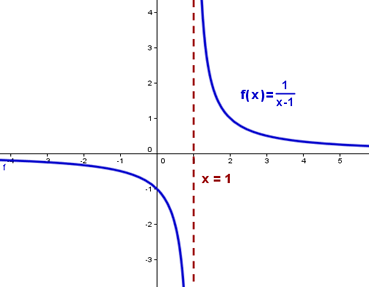
Observa la gráfica de la función f(x), en x=1 presenta una asíntota vertical, ya que la función se aproxima cada vez más a la recta vertical x=1 cuando x tiende a 1.

En el caso de funciones elementales, son candiatos a asíntotas verticales aquellos puntos aislados que no forman parte del dominio, esto no quiere decir que no haya una asíntota vertical en un punto que pertenezca al dominio de la función.
La función tiene una asíntota vertical en x=2, aunque existe f(2).
Gráfica de la función a trozos

La determinanción de las asíntotas verticales es importante para el estudio global de una función pues permite observar el comportamento su comportamiento cuando toma valores muy próximos a la asíntota.

Halla las asíntotas verticales de la función
Estamos ante una función racional, los puntos candidatos a ser asíntotas son aquellos que anulen el denominador.

Estudiamos los límites laterales en esos puntos, basta con que uno de los límites laterales tienda a infinito para que exista la asíntota vertical.

Gráfica de la función

Halla la o las asíntotas verticales de la función
¿Cuántas asíntotas verticales hay? 0 1 2 3 4