Muestreo e inferencia estadística

Cálculo de probabilidades en N(0,1) usando tabla

Para realizar estos cálculos hay que tener presente que:
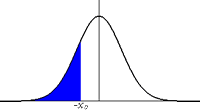
-La N(0,1) es simétrica respecto del eje de ordenadas esto significa que el área que hay bajo la curva, desde menos infinito hasta un punto -x₀ <0 es la misma que la que hay desde x₀ hasta infinito.
=
- Vamos a ayudarnos de una tabla en la que aparecen los datos para valores positivos (ver tabla)
En esa tabla la primera columna de la izquierda hace referencia a las unidades y las décimas, mientras que la primera fila nos da las centenas. Así P[ Z 1.34] = 0.9099

1. Conocemos los puntos entre los que queremos calcular la probabilidad.

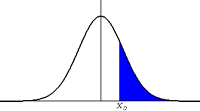
a) Cálculo de P[ Z k ]

k > 0. En este caso P[ Z k ] = F (k), se busca directamente el valor en la tabla.
Ejemplo: Calculemos la P[ Z 2.32].
Acudimos a la tabla y P[ Z 2.32]=0.9898

k < 0. Para este caso no se dispone directamente del valor en la tabla, pero gracias a la simetría de la distribución podemos afirmar que
P[ Z k ] =1 - P[ Z -k ].
Ejemplo: Calculamos P[ Z -0.5 ]
P[ Z -0.5] =1 - P[ Z 0.5 ] = 1 -0.6915 = 0.3085

b) Cálculo de P[ Z k ]

k > 0. En este caso P[ Z k ] = 1 - P[ Z k ]
Ejemplo: Calculemos la P[ Z 0.67].
P[ Z 0.67 ] = 1 - P[ Z 0.67 ] = 1 - 0.7486 = 0.2514

k < 0. P[ Z k ] = P[ Z -k ].
Ejemplo: Calculamos P[ Z -0.25 ]
P[ Z -0.25] = P[ Z 0.25 ] = 0.5987

c)Cálculo de P[ k₁ Z k₂ ]

Basta con saber que P[ k₁ Z k₂ ] = P[ Z k₂ ] - P[ Z < k₁ ]. Tenemos una diferencia de dos probabilidades que se resuelven a través de los apartados estudiados.
Ejemplo: Calculamos P[ -0.3 Z 1.2 ]
P[ -0.3 Z 1.2 ] = P[ Z 1.2 ] - P[ Z < -0.3 ] =
P[ Z 1.2 ] - (1- P[ Z < 0.3 ]) =
P[ Z 1.2 ] - 1 + P[ Z < 0.3 ] = 0.8849 - 1 + 0.6179 = 0.5028

2. Conocemos la probabilidad y hay que determinar los puntos

a) Hallar k tal que P[ Z k ]= n, donde n es un número conocido

n > 0.5 Se busca directamente en la tabla
Ejemplo: P[ Z k ]= 0.9382. Buscamos en las tablas el valor de k y és es 1.54.
Luego P[ Z 1.54 ]= 0.9382

n < 0.5. Si n es menor que 0.5 entonces el valor que buscamos es negativo.
P[ Z k ]= n es quivalente a P[ Z -k ]= n y esto es lo mismo que decir que
P[ Z -k ]=1- n
Ejemplo: P[ Z k ]= 0.33 es equivalente a P[ Z -k ]= 0.33
luego P[ Z -k ] = 0.67
Buscamos en la tabla y -k = 0.44, podemos afirmar que k = -0.44.

b) Conocemos la probabilidad que hay entre dos extremos y uno de los extremos, hay que calcular el otro.

P[ k Z k₂ ]=n o P[ k₁ Z k ]=n donde se conocen n y k₁ o k₂ y nuestra incógnita es k
Ejemplo: P[ k Z 1.12 ] = 0.5314
P[ k Z 1.12 ] = P[ Z 1.12 ] - P[ Z < k₁ ] =
P[ Z 1.12 ] - 1 + P[ Z < -k₁ ] =
0.8686 - 1 + P[ Z < -k₁ ] = 0.5314 => P[ Z < -k₁ ] = 0.6628 buscamos en la tabla y se tiene que -k = 0.42, luego k = -0.42