Progresiones aritméticas

Una sucesión se dice que está en progresión aritmética si dos términos consecutivos cualesquiera distan una misma cantidad a la que se llama diferencia.
Se tiene que $\fs2\;d=a_{n+1}-a_n\;\;n=1,2,3,4,...$

2,4,6,8,10,12,..... d=2
6,3,0,-3,-6,-9,..... d=-3

Término general
En una progresión aritmética se tiene que
$\fs2a_2=a_1+d$
$\fs2a_3=a_2+d=a_1+d+d=a_1+2d$
$\fs2a_4=a_3+d=a_1+2d+d=a_1+3d$
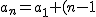Se intuye la ley de recurrencia que se sigue $\fs2a_n=a_1+(n-1)d$
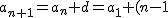Comprobemoslo para n+1 $\fs2a_{n+1}=a_n+d=a_1+(n-1)d+d=a_1+nd$
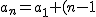Se tiene que el término general de una progresión aritmética es $\fs2a_n=a_1+(n-1)d$ ,-
Término general a partir del primer término y la diferencia.
El cálculo del término general, conocidos el primer término de la sucesión y la diferencia es sencillo, simplemente hay que sustituir en la fórmula anterior y despejar. Observa el ejemplo.

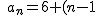En la sucesión $\fs2\;6,3,0,-3,...\;a_1=6\;y\;d=-3\;$ luego el término general de la sucesión es $\fs2\;a_n=6+(n-1)\cdot(-3)\;\Rightarrow\;a_n=6-3n+3\;\Rightarrow\;a_n=-3n+9$

Halla el término general de una progresión aritmética de la que se sabe que
$a_1=-5\;y\;\;d=8$

Solución $\fs3a_n=$

Nota:La solución debe estar simplificada, como en el ejemplo, para que el corrector reconozca la fórmula.

Ec. primer grado	Fracciones	Potencias	Enteros	Factor común	Monomios	Aproximación	Figuras planas	Triángulos Rectángulos
Problemas - ecuaciones	Triángulos	Divisibilidad	Ecuación de segundo grado		Naturales	Decimales	Proporcionalidad	Identidades Notables

Ec. primer grado	Fracciones	Potencias	Enteros	Factor común	Monomios	Aproximación	Figuras planas	Triángulos Rectángulos
Problemas - ecuaciones	Triángulos	Divisibilidad	Ecuación de segundo grado		Naturales	Decimales	Proporcionalidad	Identidades Notables

Fracciones	Triángulos	Ec. Primer Grado	Polinomios	Resol. Sist. Ecuaciones	Cálculo ecuación recta	Parábola	Radicales
Divisibilidad	Monomios	Ecuación recta	Id. Notables	Triángulos Rectángulos	Pendiente de una recta	Factor común	Sucesiones
Potencias	Inecuaciones	Cálculo de la pendiente	Problemas	Prob. Sist. Ecuaciones	Ec. segundo grado	Aproximación

Potencias	Resol. Sist. Ecuaciones	Parábola	Racionalización	Progresiones aritméticas		Ec. Exponencial
Inecuaciones	Ec. segundo grado	Polinomios	Ec. Irracional	Progresiones geométricas		Identidades Notables
Logaritmos	Prob. Sist. Ecuaciones	Factor común	Operaciones con Radicales	Trigonometría	Raíces	Ec. Logarítmica

Ec. recta en el plano	Ec. Exponencial	Prog. aritméticas	Límite en un punto	Ec. Irracional	Logaritmos	Inecuaciones
Posición relativa dos rectas	Ec. Logarítmica	Prog. geométricas	Límite en el infinito	Asíntotas	Continuidad	Factor común
Gráfica y expresión analítica	Sistemas 3 ecuaciones	Prod. escalar	Trigonometría	Distancias	Dominios

Ec. recta plano	Distancias	Ec. recta espacio	Ec. Irracional	Pos. rel.dos rectas	Pos. rel. tres planos
Posición relativa dos rectas	Determinantes	Ec. Plano espacio	Logaritmos	Pos. rel. recta-plano	Continuidad
Sistemas 3 ecuaciones	Matrices	Ángulo	Prod. escalar	Pos. rel dos planos	Dominios

Tablas estadísticas	Gráficas	Medidas descriptivas	Variables bidimensionales
Probabilidad	Variable Aleatoria	Inferencia

Número factorial	Variaciones ordinarias	Variaciones con repetición	Permutaciones ordinarias	Permutaciones circulares
Permutaciones con repetición	Números combinatorios	Combinaciones ordinarias	Combinaciones con repetición	Ejercicios de Combinatoria