Consideremos la función definida en R, los candidatos a asíntotas verticales son aquellos valores que no están en el dominio de f. En nuestro caso son x=2 y x=3. Para que en estos puntos haya una asíntota vertical tiene que ocurrir que alguno de los límites laterales sea infinito. En este ejemplo tanto cualquiera de los límites laterales tanto en x=2 como en x=3 es infinito. Podemos afirmar que las rectasx=2 y x=3 son aísntotas verticales de la función dada.

Consideremos la función definida en R, la recta y=a será una asíntota horizontal de la función f si es el límite de f cuando tiende a mas o menos infinito. Luego para determinar la o las asíntotas horzontales de una función hallamos los límites en infinito de la función. En nuestro ejemplo el grado del polinomio del denominador es mayor que el del numerador, por tanto el límite de f es 0. La recta y=0 es la asíntota horizontal de la función dada.

Consideremos la función definida en R.
Una recta y=mx+n es asíntota oblicua de f si el límite en infinito de [f(x)-(mx+n)]=0.
Hemos de determinar m y n para ello primero calculamos .
Una vez determinado m se calcula
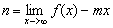
, y ahora calculamos
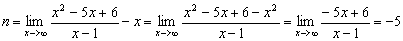
La recta y=x-5 es una asíntota oblicua de f.