Consideremos las rectas y , el ángulo que formen estas rectas será el ángulo que formen sus vectores de dirección. La recta r viene dada por la intersección de dos planos, el vector de dirección de la recta es perpendicular a los vectores normales de los planos, podemos determinarlo a partir del producto vectorial.

equivalentemente
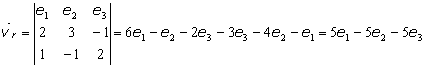Razonando análogamente con la recta s se llega a que un vector de dirección es u=(-4,-3,-3)
El ángulo que forman las rectas vendrá dado por la fórmula del producto escalar
=>

Dados dos planos de ecuación general 2x+3y-z+5=0 y -x+5y-z+3=0, el ángulo que formen será el mismo que el que forman sus vectores normales, que respectivamente son (2,3,-1) y (-1,5,1). Recurriendo nuevamente a la fórmula del producto escalar se tiene que
=>

El ángulo que forman una recta y un plano es complementario al que forman el vector normal del plano y el de dirección de la recta. Además la relación entre dos ángulos complementarios permite afirmar que el coseno de uno es el seno del otro. Por tanto el ángulo vendrá dado por la fórmula donde n es el vector normal del plano y v el vector de dirección de la recta.

Consideremos la recta y el plano de ecuación general -x+5y-z+3=0, la recta de este ejemplo es la misma que la del primero por tanto su vector de dirección ya está calculado y es (1,-1,-1), el normal del plano (-1,5,-1) .
Aplicando la fórmula anterior se tiene que =>